Introduction
Sudoku 4×4 is a puzzle game which we have to determine the place of numbers by using given hints under some rules. Here we explain the rule of Sudoku 4×4 in detail for those who plays it for the first time. Then we demonstrate the solving process of an example puzzle.
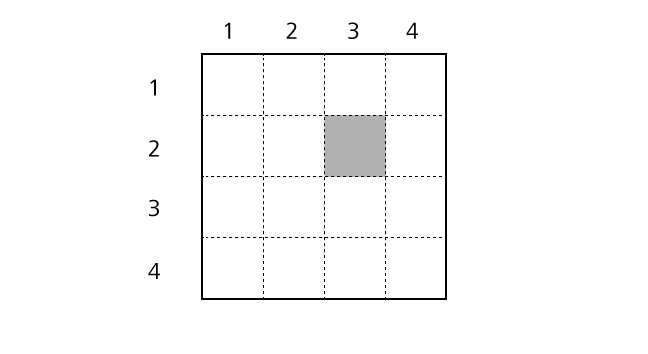
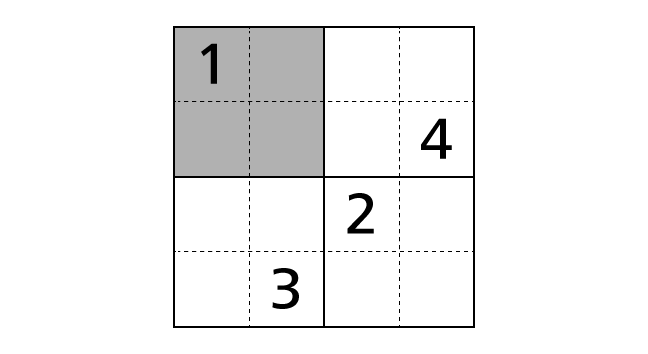
In explanations, we call a horizontal sequence of boxes row and a vertical sequence of boxes column. We describe a position of a box as (1,1) using a row and a column number. For example, we call the colored box in the following image box–(2,3).
Rule
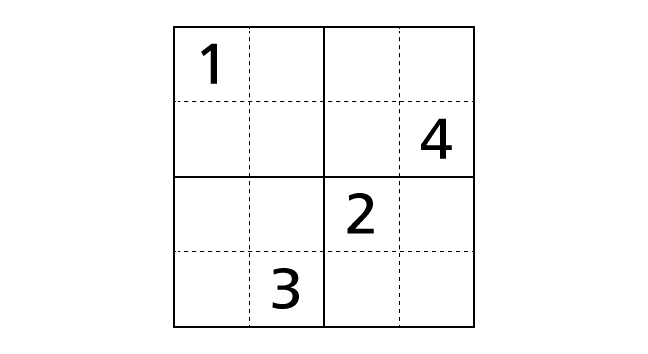
There are three rules for Sudoku 4×4. Please remember them all.
- Each row contains each digit of 1–4 exactly once.
- Each column contains each digit of 1–4 exactly once.
- Each region surrounded by thick lines contains each digit of 1–4 exactly once.
Now we explain each rule in detail by using the example puzzle following.
Rule 1
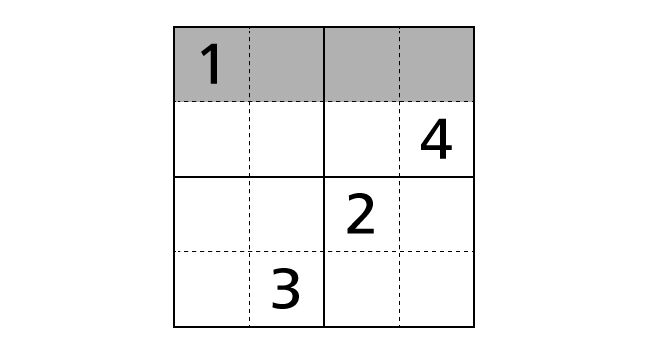
Each row contains each digit of 1–4 exactly once. This means that we cannot place same numbers in a row. In the example, a number 1 is placed in box–(1,1). So we cannot place another number 1 in box–(1,2), box–(1,3) and box–(1,4).
Rule 2
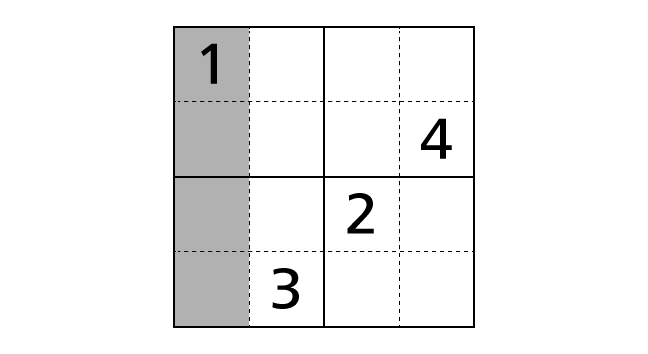
Each column contains each digit of 1–4 exactly once. This means that we cannot place same numbers in a column. In the example, a number 1 is placed in box–(1,1). So we cannot place another number 1 in box–(2,1), box–(3,1) and box–(4,1).
Rule 3
Each region surrounded by thick lines contains each digit of 1–4 exactly once. This means that we cannot place same numbers in a region. In the example, we can see four regions. Box–(1,1), box–(1,2), box–(2,1) and box–(2,2) forms one regions. A number 1 is placed in box–(1,1). Then we cannot place another number 1 in box–(1,2), box–(2,1) and box–(2,2).
Tutorial
Here, we demonstrate a solving process of the example puzzle. This is not the only process to solve. We hope you will find other processes.
Process 1
A basic technique to solve Sudoku 4×4 is to find boxes in which a specific number should be placed. For that, we focus on given hints. First, we focus on a number 1 of box–(1,1). We fill boxes in which we cannot place a number 1 with a color by following rules.
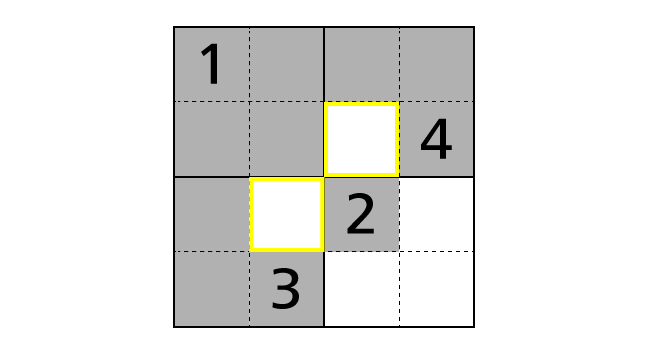
This time, we notice that there is a box (surrounded by yellow lines) that number 1 is the only choice to be placed in. Because, by rule 3, we have to place a number 1 exactly once in the top right region. But, by rule 1, we cannot place a number 1 in box–(1,3) and box–(1,4). So box–(2,3) is the only box that we can place a number 1 in.
As the same way, in the bottom left region, box–(3,2) is the only box that we can place a number 1 in.
Now let’s place numbers.
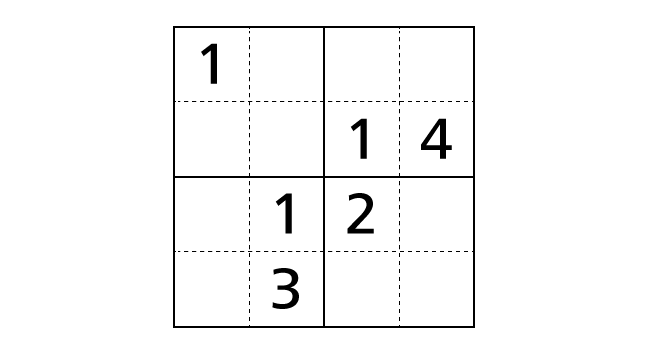
Process 2
Next, we focus on number 2 in box–(3,3). Then we fill boxes in which we cannot place a number 2 with a color by following rules.

We noticed that there are boxes that number 2 is the only choice to be placed in. Now let’s place numbers.
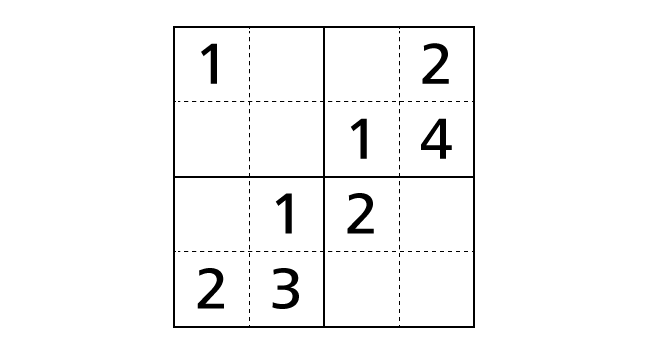
Process 3
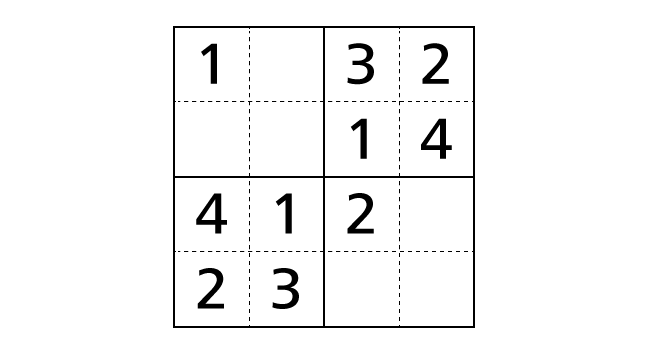
Next, we focus on the top right region and the bottom left region. Then, by rule 3, we notice that box–(1,3) is the only box that we can place a number 3 in. Moreover, by rule 3, we notice that box–(3,1) is the only box that we can place a number 4 in.

Now let’s place numbers.
Process 4
Next, we focus on row 1. Then, by rule 1, we know that each row contains each digit of 1–4 exactly once. But number 1, 2 and 3 are already placed in row 1. So box–(1,2) is the only box that we can place a number 4 in.
As the same way, by focusing on row 3, we notice that box–(3,4) is the only box that we can place a number 3 in.

Now let’s place numbers.

Process 5
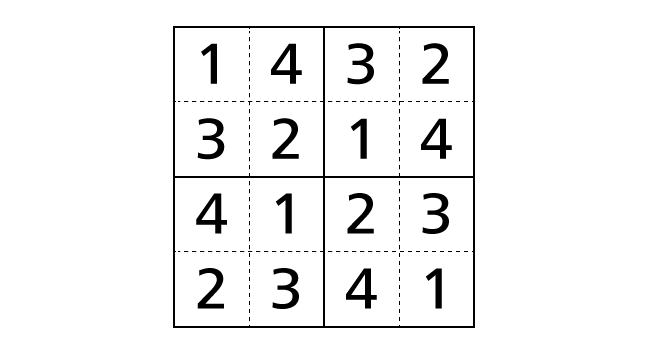
Next, we focus on column 1. Then, by rule 2, we know that each column contains each digit of 1–4 exactly once. But number 1, 2 and 4 are already placed in column 1. So box–(2,1) is the only box that we can place a number 3 in.
As the same way, by focusing on columns, we can place numbers in right boxes.

Finally, we reached the answer.
Get Started
Most recently uploaded Sudoku 4×4 puzzles are available on Sudoku 4×4.
Previous Sudoku 4×4 puzzles are available on Sudoku Archives.
