Introduction
When we play Skyscrapers Puzzle, we assume that we are watching the buildings with heights of 1–4 from above.
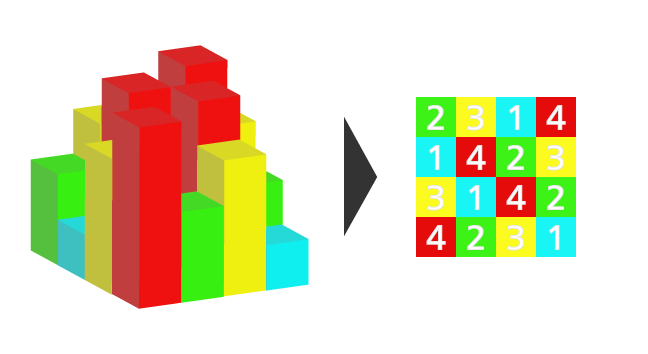
Skyscrapers Puzzle is a puzzle game which we have to determine the place of numbers by using given hints under some rules.
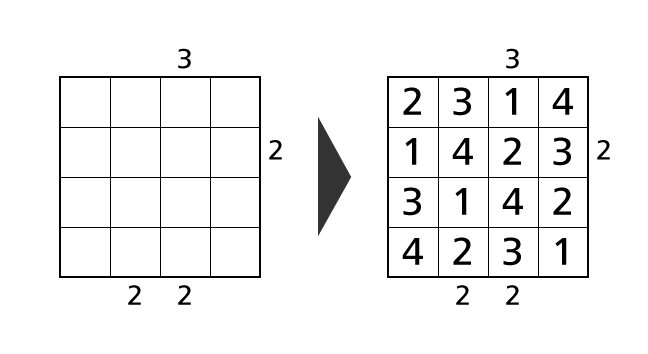
Here we explain the rule of Skyscrapers Puzzle with size 4×4 in detail for those who plays it for the first time. Then we demonstrate the solving process of an example puzzle.
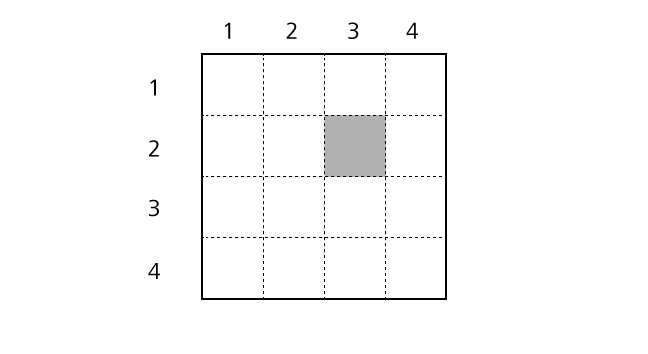
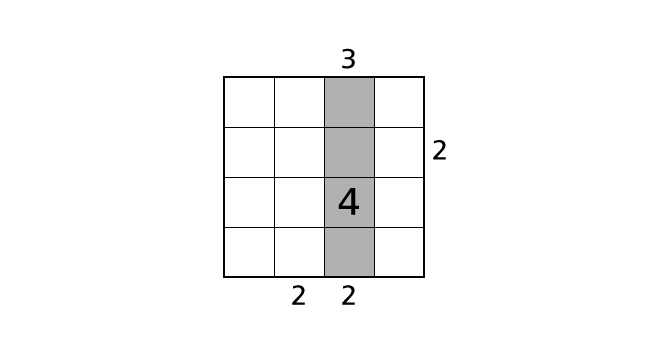
In explanations, we call a horizontal sequence of boxes row and a vertical sequence of boxes column. We describe a position of a box as (1,1) using a row and a column number. For example, we call the colored box in the following image box–(2,3).
Rule
There are three rules for Skyscrapers Puzzle. Please remember them all.
- Each row contains each digit of 1–4 exactly once.
- Each column contains each digit of 1–4 exactly once.
- Digits outside of the grid indicate how many buildings we can see from that point.
Now we explain each rule in detail by using the example puzzle above.
Rule 1
Each row contains each digit of 1–4 exactly once. This means that we cannot place same numbers in a row. After deliberation, in the example puzzle, we know that we have to place a number 4 in box–(3,3). So, by this rule, we cannot place another 4 in row 3.
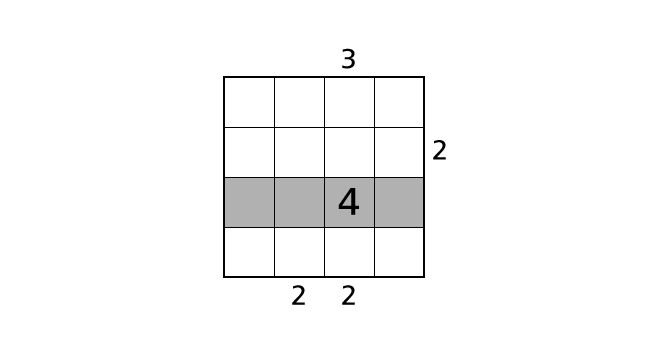
Rule 2
Each column contains each digit of 1–4 exactly once. This means that we cannot place same numbers in a column. So, in the example puzzle, we cannot place another 4 in column 3.
Rule 3
Digits outside of the grid indicate how many buildings we can see from that point. By using this information as hints, we will decide the place of numbers.
Higher buildings hide lower buildings. Now we assume that four buildings are lined up in order like in the image below. Then, if we watch buildings from the left side, we can see only one building. If we watch buildings from the right side, we can see four buildings.
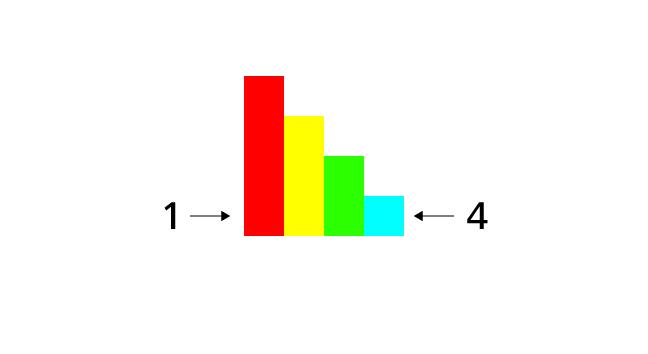
When we see four buildings from a direction, we know that buildings are lined up in order of increasing height from the direction. Because if buildings are lined up in other order, we can never see all four buildings.
When we can see only one building, we know that a building with height 4 is in front of us. But, we cannot decide in what order rest buildings are lined up. There are six possibilities.
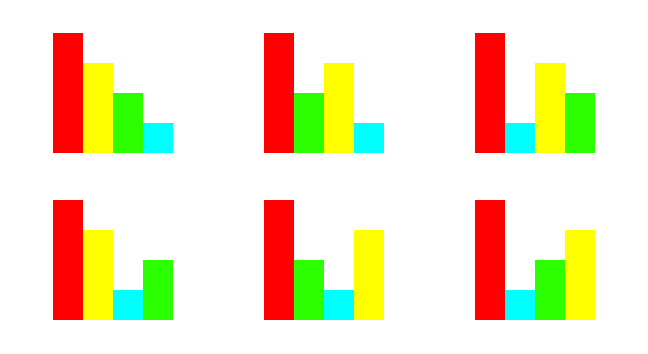
In such a case, we have to combine other hints to decide the place of numbers.
Tutorial
Here, we demonstrate a solving process of the example puzzle following. This is not the only process to solve. We hope you will find other processes.
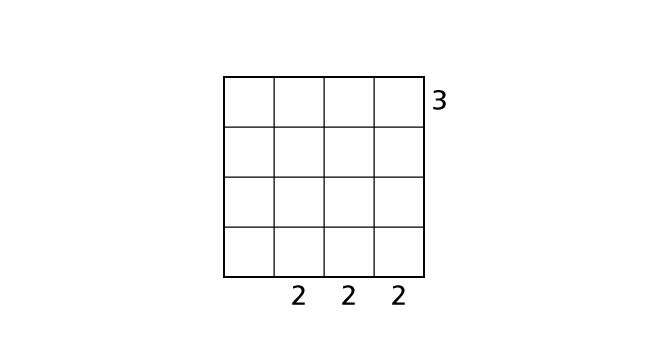
Process 1
A basic technique to solve Skyscrapers Puzzle is to decide places of number 4 first.
Now we focus on row 4. By rule 1, we can place number 4 in row 4 exactly once. Moreover, we can see only one building if a building with height 4 is in front. From these, we know that box–(4,1) is the only box in which we can place a number 4.
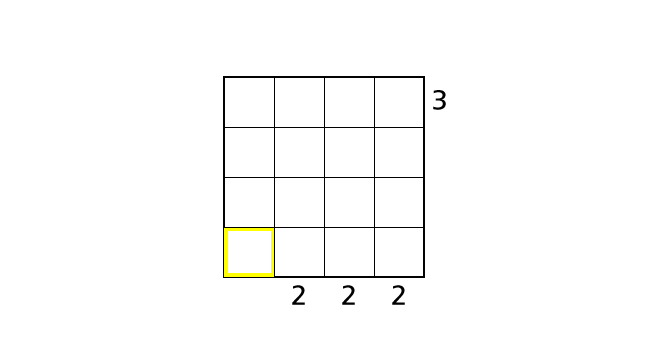
If we place a number 4 in box–(4,2), box–(4,3) or box–(4,4), we end up violating the rule 3. Now let’s place a number.
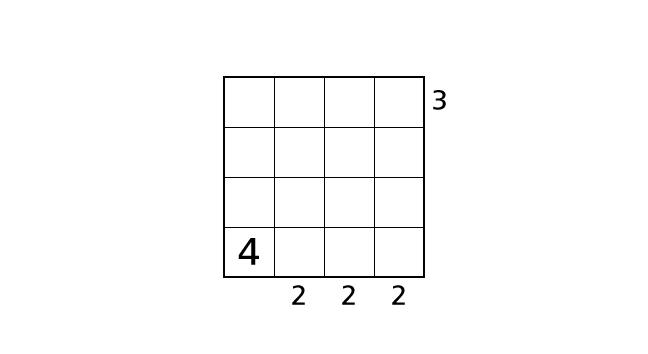
Process 2
Next, we focus on row 1. We placed a number 4 in box–(4,1) in process 1. So, by rule 2, we cannot place another number 4 in box–(1,1).
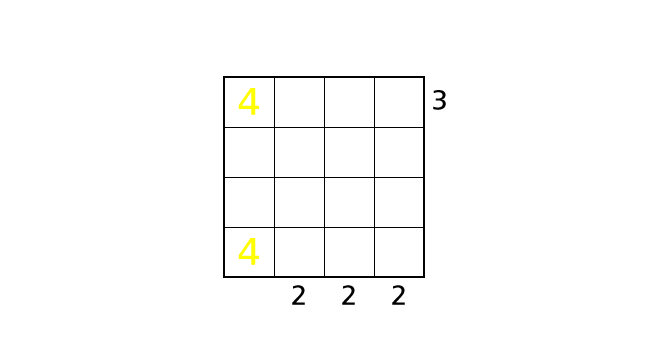
Now we assume cases that we place a number 4 in box–(1,3) and box–(1,4) respectively.
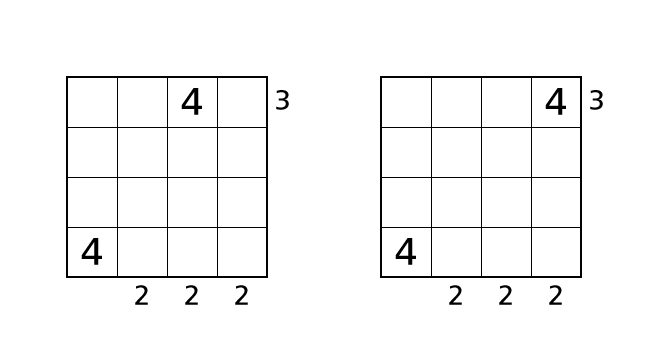
In both of these cases, we cannot see three buildings from the right side. Thus, we end up violating the rule 3. So we know that box–(1,2) is the only box in which we can place a number 4. Let’s place a number.
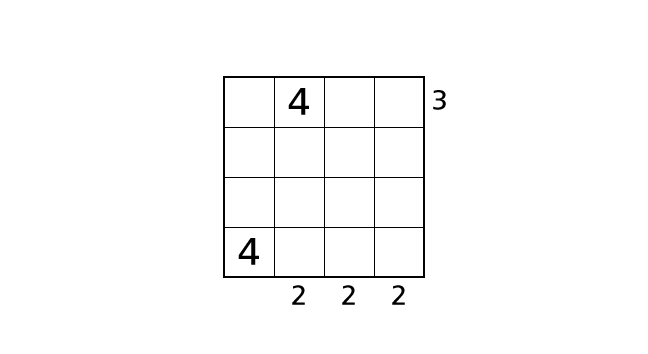
Process 3
We cannot decide places of number 4 anymore. So we think of places of number 3.
Now we focus on column 2. We have three boxes in which we can place a number 3. We assume cases that we place a number in box–(2,2) and box–(3,2) respectively.
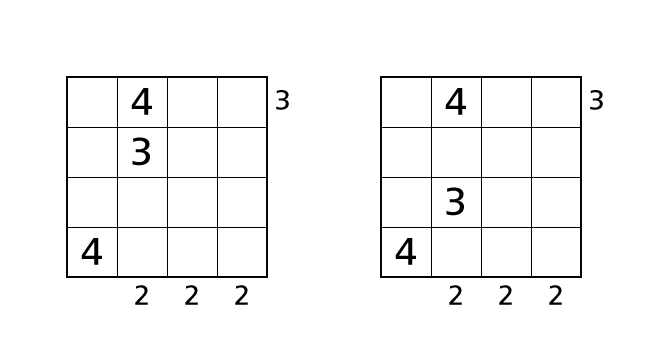
In both of these cases, we can see greater than two buildings no matter how we line up rest buildings. So we end up violating the rule 3 in these cases. Thus we know that box–(4,2) is the only box in which we can place number 3. Let’s place a number.
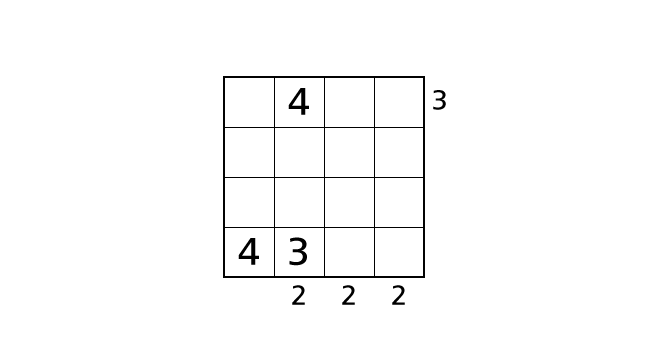
Process 4
We cannot decide places of number 3 anymore. So we think of two possible cases that we place number 4 so that we don’t violate the rules.
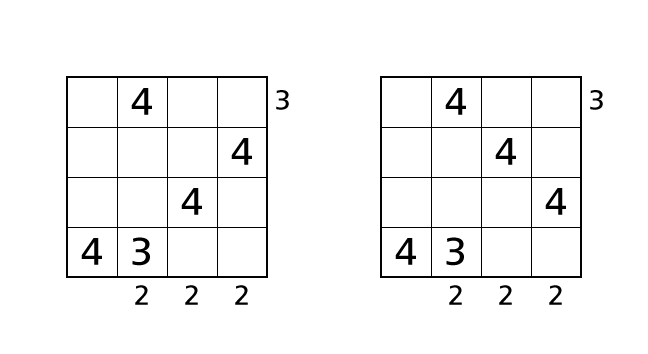
Here we think of the first case. We focus on column 4. We can place a number 3 in box–(1,4), box–(3,4) or box–(4,4).
First, if we place a number 3 in box–(1,4), we can see two buildings from the right side. So we end up violating rule 3. Next, if we place a number 3 in box–(4,4), we see number 3 twice in row 4. So we end up violating rule 1.
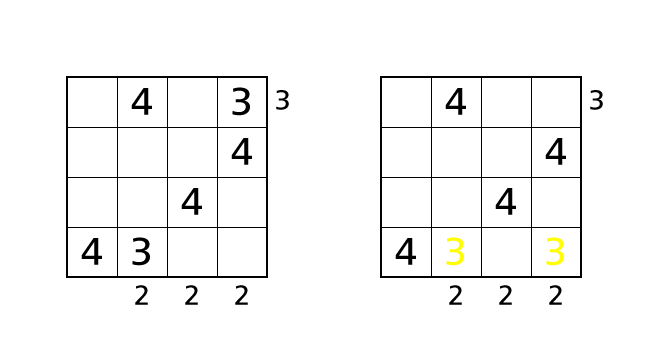
Finally, if we place a number 3 in box–(3,4), we can see three buildings from the bottom side no matter how we line up rest buildings. Again, we end up violating rule 3.
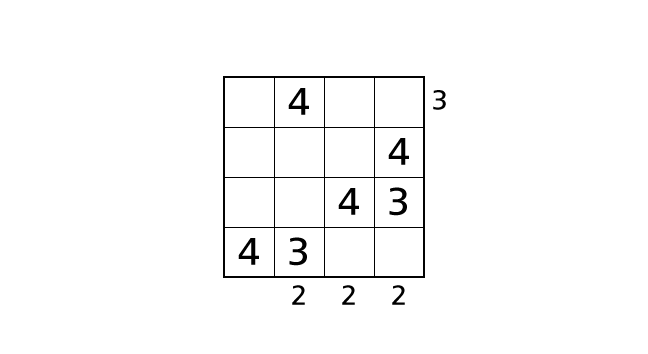
In all of these cases, we end up violating the rules. This is due to the wrong choice of the place of number 4. So we think of the other case from now.
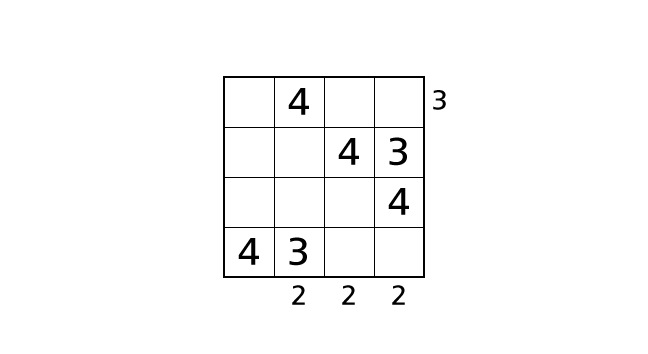
Process 5
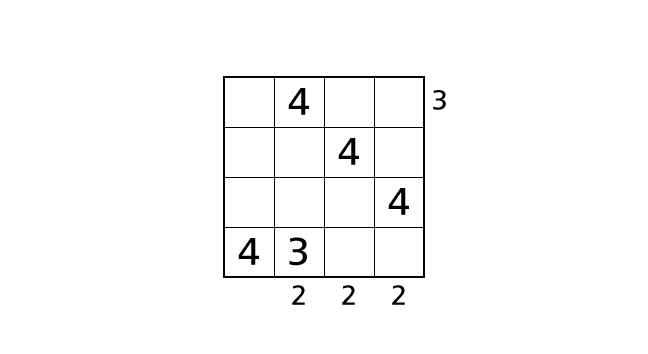
Now we focus on column 4. We can place a number 3 in box–(1,4), box–(2,4) and box–(4.4).
First, if we place a number 3 in box–(1,4), we can see two buildings from the right side. So we end up violating rule 3. Next, if we place a number 3 in box–(4,4), we see number 3 twice in row 4. So we end up violating rule 1.
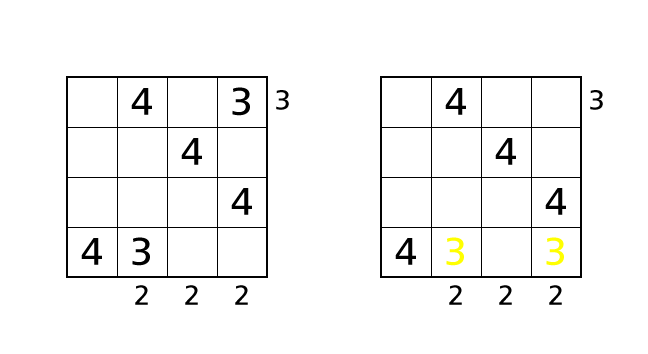
So we know that box–(2,4) is the only box in which we can place a number 3. Let’s place a number.
Process 6
Now we focus on column 3. We can place a number 3 in box–(1,3), box–(3,3) and box–(4,3).
First, if we place a number 3 in box–(3,3), we can see three buildings from the bottom side no matter how we line up rest buildings. So we end up violating the rule 3. Next, if we place a number 3 in box–(4,3), we see number 3 twice in row 4. So we end up violating the rule 1.
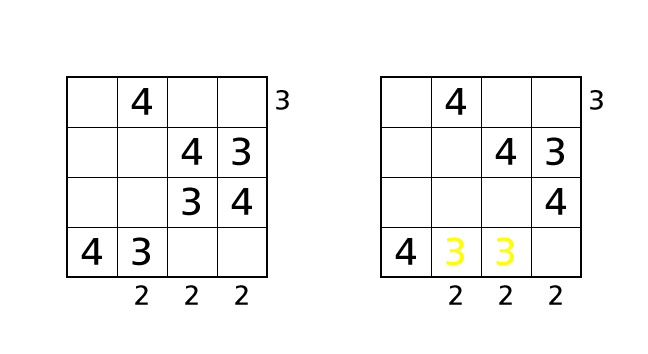
So we know that box–(1,3) is the only box in which we can place a number 3. Let’s place a number.
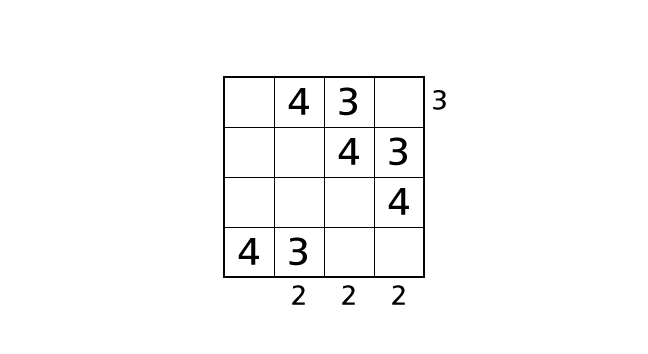
Process 7
Now we focus on column 1. We can place a number 3 in box–(1,1), box–(2,1) and box–(3.1).
If we place a number 3 in box–(1,1) or box–(2,1), in both cases, we end up violating the rule 1.
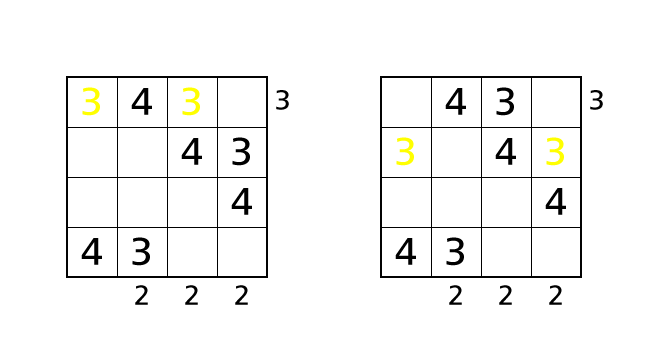
So we know that box–(3,1) is the only box in which we can place a number 3. Let’s place a number.
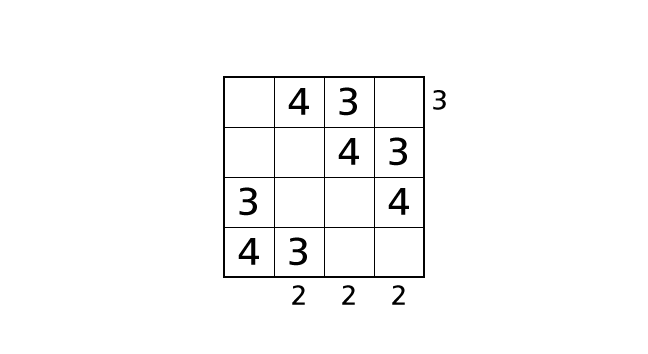
Here we have placed all of number 3 and number 4. We think of places of number 1 and number 2 from now.
Process 8
Now we focus on column 3. We assume the case that we place a number 1 in box–(4,3) and a number 2 in box–(3,3).
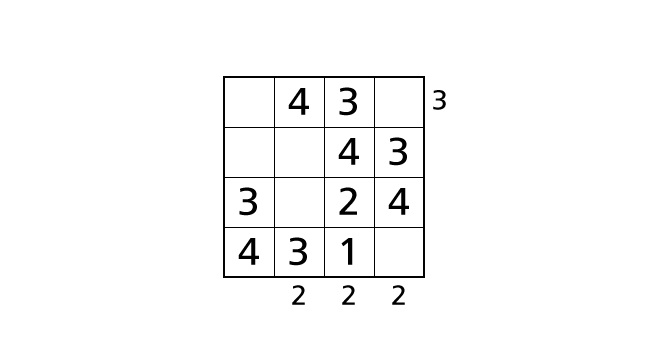
In this case, we can see three buildings from the bottom side. So we end up violating the rule 3. Thus we have to place a number 1 in box–(3,3) and a number 2 in box–(4,3) to avoid violating the rule 3. Let’s place numbers.
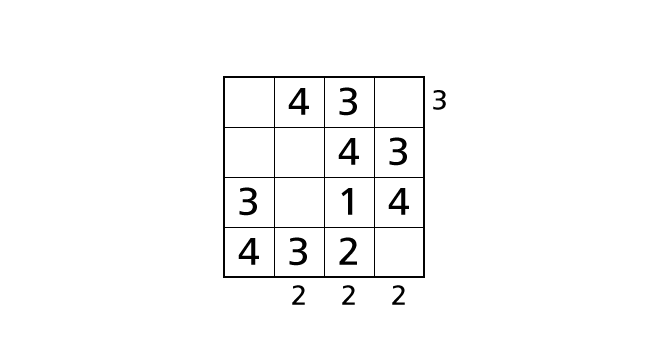
Process 9
Now we focus on row 3 and row 4. By rule 1, we know that each row contains each digit of 1–4 exactly once. So we have to place a number 2 in box–(3,2) and a number 1 in box–(4,4). Let’s place numbers.
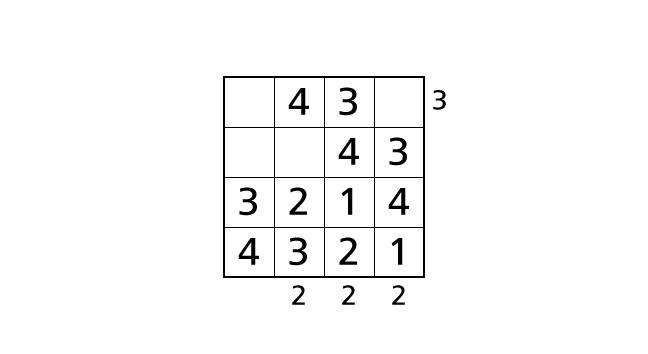
Next, we focus on column 2 and column 4. By rule 2, we know that each column contains each digit of 1–4 exactly once. So we have to place a number 1 in box–(2,2) and a number 2 in box–(1,4). Let’s place number.
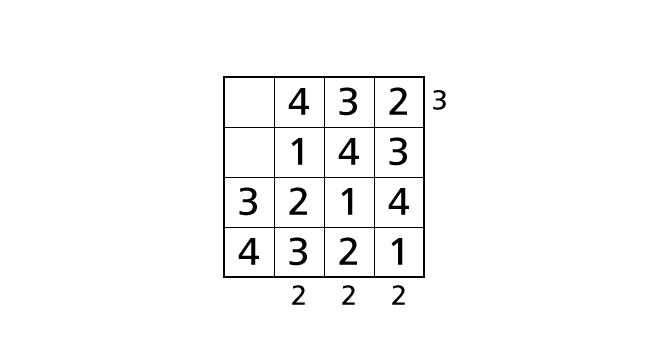
Finally, we focus on row 1 and row 2. Again, by rule 1, we know that each row contains each digit of 1–4 exactly once. So we have to place a number 1 in box–(1,1) and a number 2 in box–(2,1). Then we reached the answer.

Get Started
Most recently uploaded Skyscrapers puzzles are available on Skyscrapers Puzzle.
Previous Skyscrapers puzzles are available on Skyscrapers Puzzles Archives.
