Introduction
CalcBlocks is a puzzle game which we have to determine the place of numbers by using given hints under some rules. Here we explain the rule of CalcBlocks with size 4×4 in detail for those who plays it for the first time. Then we demonstrate the solving process of an example puzzle.
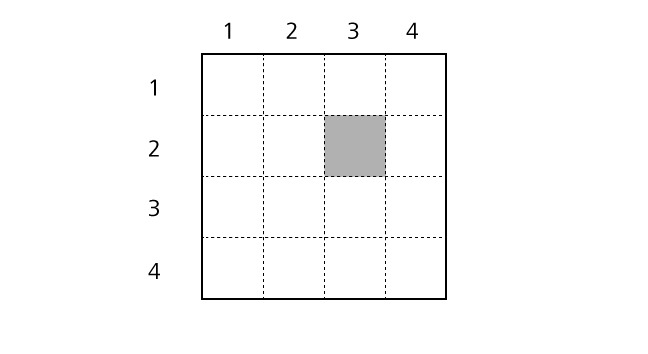
In explanations, we call a horizontal sequence of boxes row and a vertical sequence of boxes column. We describe a position of a box as (1,1) using a row and a column number. For example, we call the colored box in the following image box–(2,3).
Rule
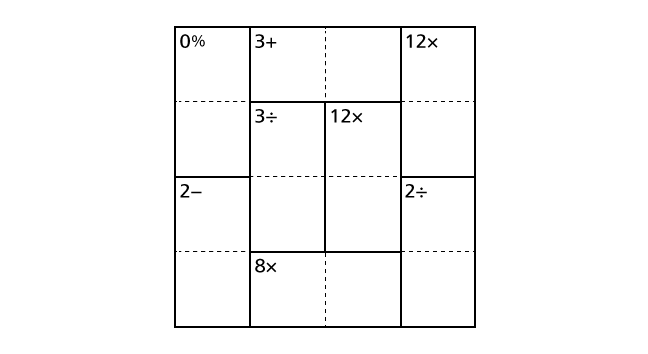
There are three rules for CalcBlocks. Please remember them all. Here, we use a word operator. Operator is a symbol or function denoting an operation (e.g., ×, +).
- Each row contains each digit of 1–4 exactly once.
- Each column contains each digit of 1–4 exactly once.
- A number and an operator in each region surrounded by thick lines denote the addition of numbers (+), the difference of two numbers (–), the product of numbers (×), the quotient of bigger number / smaller number (÷) or the remainder of bigger number / smaller number (%).
Now we explain each rule in detail by using the example puzzle following.
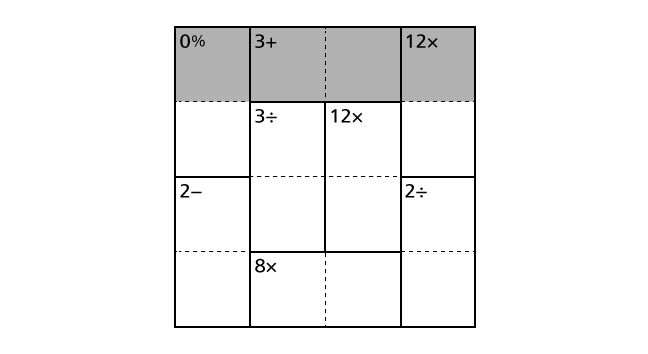
Rule 1
Each row contains each digit of 1–4 exactly once. This means that we cannot place same numbers in a row.
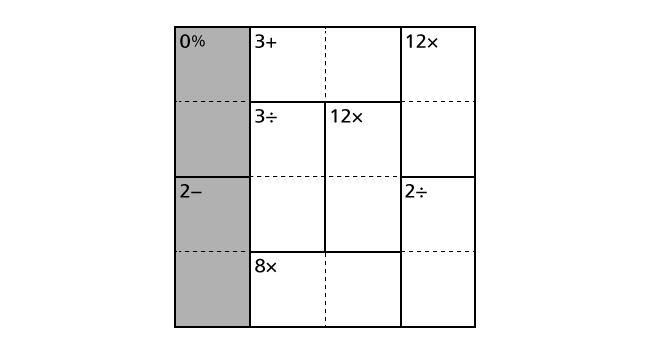
Rule 2
Each column contains each digit of 1–4 exactly once. This means that we cannot place same numbers in a column.
Rule 3
A number and an operator in each region surrounded by thick lines denote the addition of numbers (+), the difference of two numbers (–), the product of numbers (×), the quotient of bigger number / smaller number (÷) or the remainder of bigger number / smaller number (%).
Addition
In the example, we can see 3+ in the top center region including box–(1,2) and box–(1,3).
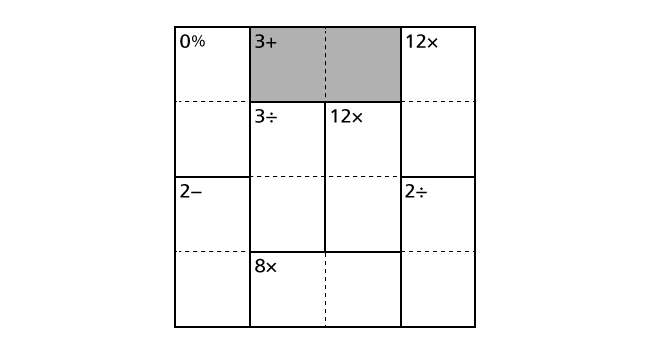
This means that 3 is the addition of two numbers that should be placed in box–(1,2) and box–(1,3). Among four numbers from 1 to 4, 1 and 2 are the only combination that the result of the addition becomes 3. Thus, from this hint, we know that we have to place a number 1 and a number 2 in box–(1,2) and box–(1,3). But, from only this hint, we cannot decide in which box to place a number 1.
Difference
In the example, we can see 2– in the bottom left region including box–(3,1) and box–(4,1).
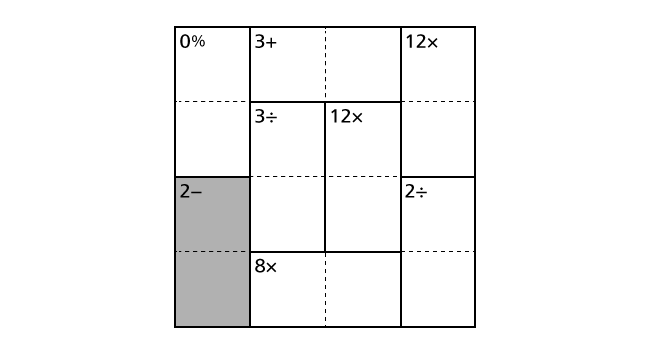
This means that 2 is the result of the difference (bigger number – smaller number) of two numbers that should be placed in box–(3,1) and box–(4,1). Among four numbers from 1 to 4, 4 and 2 or 3 and 1 are combinations that the result of the difference becomes 3. Thus, from this hint, we know that a combination of 4 and 2 or a combination of 3 and 1 should be placed in box–(3,1) and box–(4,1). But, from only this hint, we cannot decide which combination to select.
Product
In the example, we can see 12× in the top right region including box–(1,4) and box–(2,4).
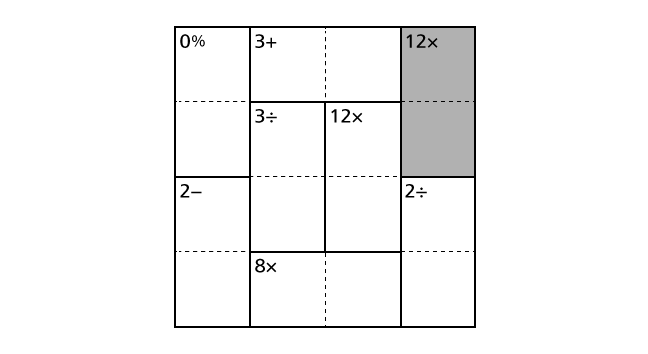
This means that 12 is the product of two numbers that should be placed in box–(1,4) and box–(2,4). Among four numbers from 1 to 4, 3 and 4 are the only combination that the result of the product becomes 12. Thus, from this hint, we know that we have to place a number 3 and a number 4 in box–(1,4) and box–(2,4). But, from only this hint, we cannot decide in which box to place a number 3.
Quotient
In the example, we can see 3÷ in the middle left region including box–(2,2) and box–(3,2).
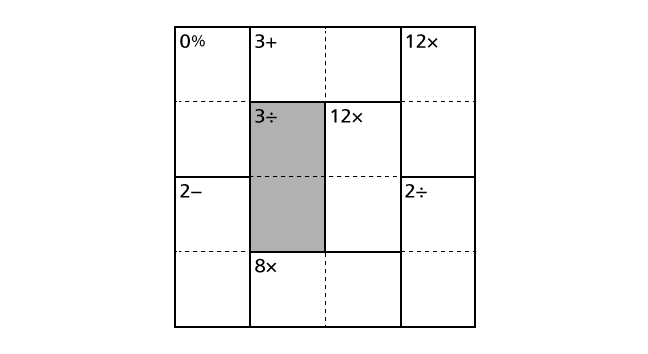
This means that 3 is the quotient of the division (bigger number / smaller number) of two numbers that should be placed in box–(2,2) and box–(3,2). Among four numbers from 1 to 4, 3 and 1 are the only combination that the result of the quotient becomes 3. Thus, from this hint, we know that we have to place a number 3 and a number 1 in box–(2,2) and box–(3,2). But, from only this hint, we cannot decide in which box to place a number 3.
Remainder
We call the operation that produces a remainder when given a dividend and divisor modulo. At first, You may think this operation difficult. But this operation is very important. Because five operations we saw are called five fundamental operations of mathematics. Moreover, the modulo operation is often used in computer programming as well. Please become familiar with this operation through playing this puzzle.
In the example, we can see 0% in the top left region including box–(1,1) and box–(2,1).
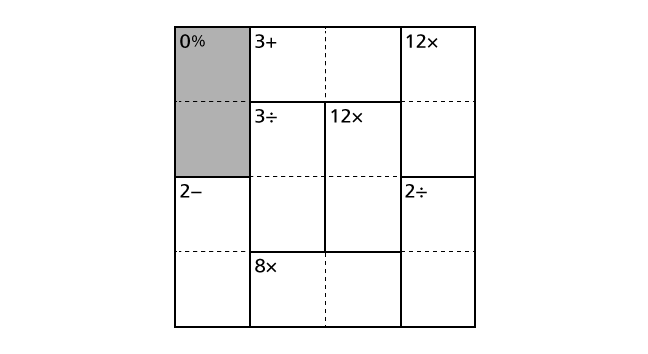
This means that 0 is the remainder of the division (bigger number / smaller number) of two numbers that should be placed in box–(1,1) and box–(2,1). Namely, the bigger number is dividable by the smaller number. Among four numbers from 1 to 4, there are four dividable combinations, 4 and 2, 4 and 1, 3 and 1 or 2 and 1. But, from only this hint, we cannot decide which combination to select.
Tutorial
Here, we demonstrate a solving process of the example puzzle following. This is not the only process to solve. We hope you will find other processes.
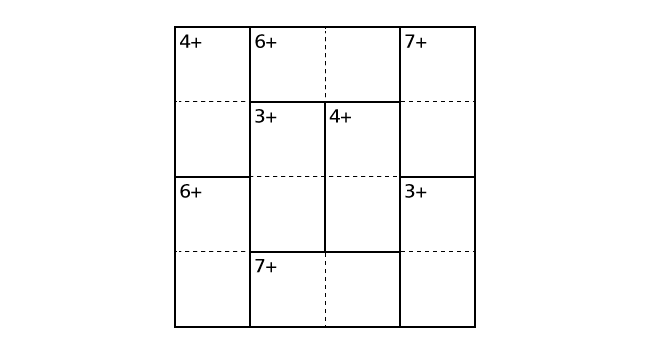
Process 1
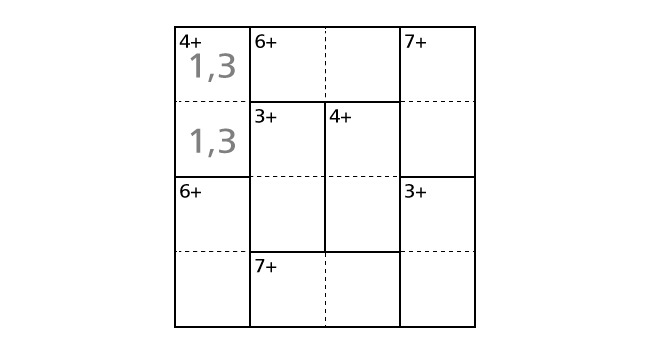
First, we focus on the top left region including box–(1,1) and box–(2,1). Among four number from 1 to 4, 1 and 3 are the only combination that the result of the addition of two numbers becomes 4. Thus, we know that we have to place a number 1 and a number 3 in box–(1,1) and box–(2,1). But, from only this hint, we cannot decide in which box to place a number 1. So now we record this in boxes with light-colored characters.
Next, we focus on the top center region including box–(1,2) and box–(1,3). Among four number from 1 to 4, 2 and 4 are the only combination that the result of the addition of two numbers becomes 6. Thus, we know that we have to place a number 2 and a number 4 in box–(1,2) and box–(1,3). But, from only this hint, we cannot decide in which box to place a number 2. So now we record this in boxes with light-colored characters.
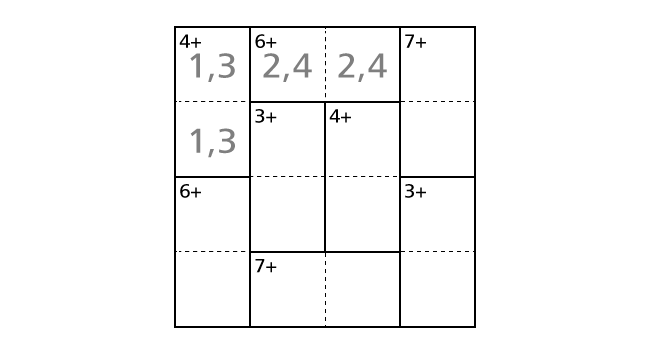
Next, we focus on the top right region including box–(1,4) and box–(2,4). Among four number from 1 to 4, 3 and 4 are the only combination that the result of the addition of two numbers becomes 7. Thus, we know that we have to place a number 3 and a number 4 in box–(1,4) and box–(2,4). But, from only this hint, we cannot decide in which box to place a number 3. So now we record this in boxes with light-colored characters.
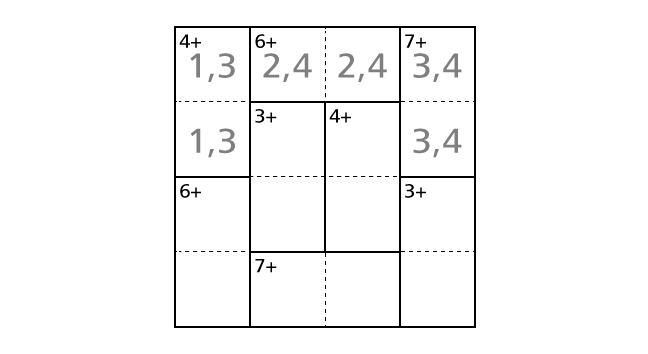
Process 2
In the top right region, we couldn’t decide in which box to place a number 3. However, by considering the fact that we have to place a number 2 and a number 4 in box–(1,2) and box–(1,3), we can decide in which box to place a number 3.
Now we assume the case that we place a number 4 in box–(1,4) and a number 3 in box–(2,4).
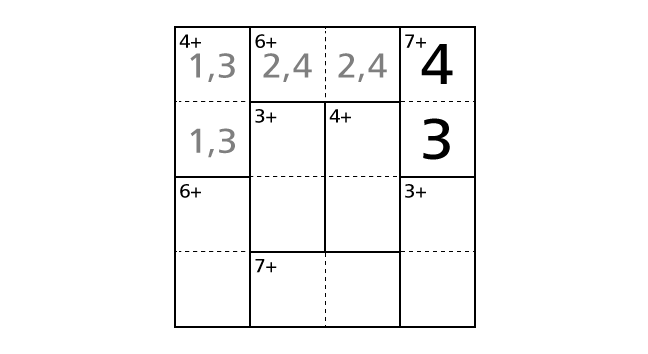
Then, we know that we have to place a number 2 and a number 4 in box–(1,2) and box–(1,3), no matter how we place a number 2 and a number 4, we end up violating the rule 1.
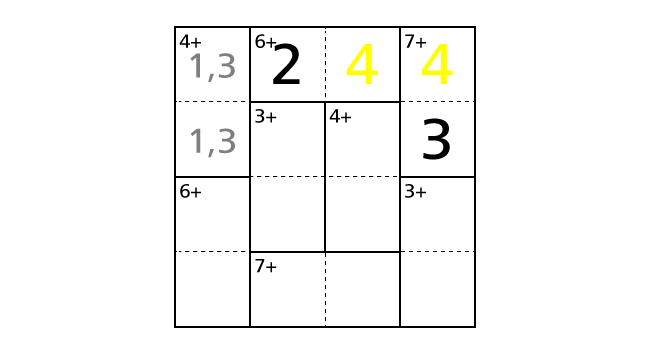
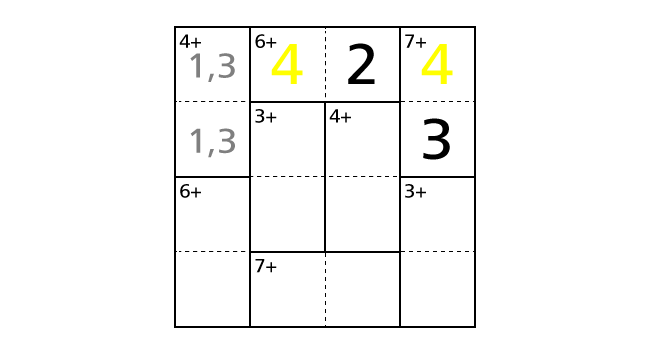
So we have to place a number 4 in box–(2,4) and a number 3 in box–(1,4) to avoid violating the rules. Now let’s place numbers.
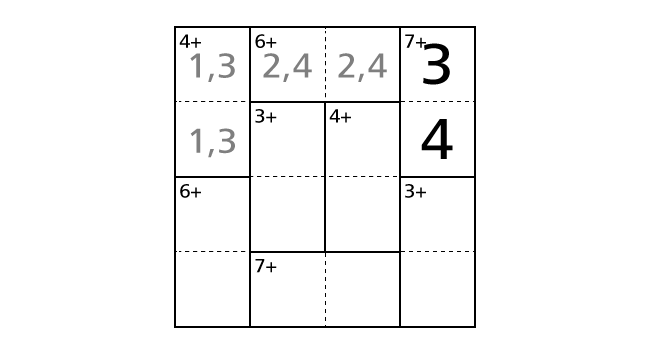
Process 3
Now we can decide in which box to place a number 1 in the top left region including box–(1,1) and box–(2,1). If we assume the case that we place a number 1 in box–(2,1) and a number 3 in box–(1,1), we notice that we end up violating the rule 1.

So we have to place a number 1 in box–(1,1) and a number 3 in box–(2,1) to avoid violating the rules. Now let’s place numbers.
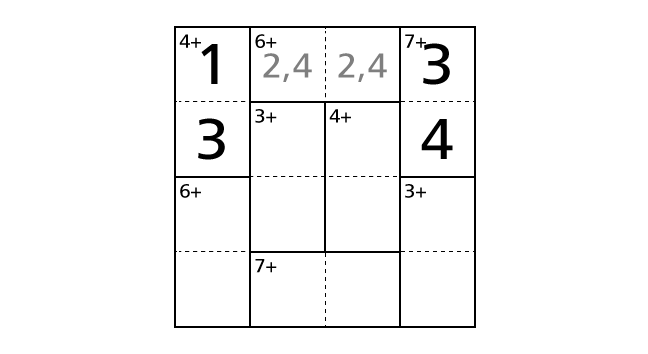
Process 4
We focus on the middle left region including box–(2,2) and box–(3,2). Among four number from 1 to 4, 1 and 2 are the only combination that the result of the addition of two numbers becomes 3. Thus, we know that we have to place a number 1 and a number 2 in box–(2,3) and box–(3,2). But, from only this hint, we cannot decide in which box to place a number 1. So now we record this in boxes with light-colored characters.
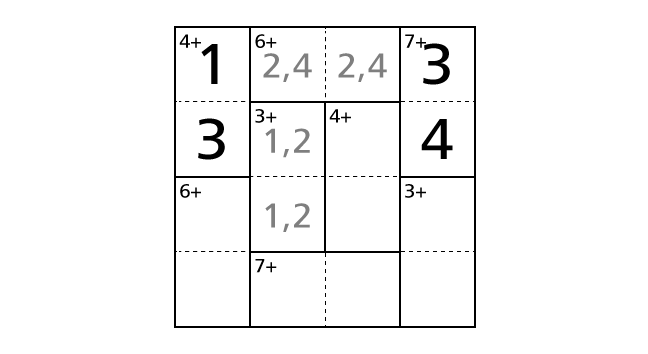
Next, we focus on the middle right region including box–(2,3) and box–(3,3). Among four number from 1 to 4, 1 and 3 are the only combination that the result of the addition of two numbers becomes 4. Thus, we know that we have to place a number 1 and a number 3 in box–(2,3) and box–(3,3). But, from only this hint, we cannot decide in which box to place a number 1. So now we record this in boxes with light-colored characters.
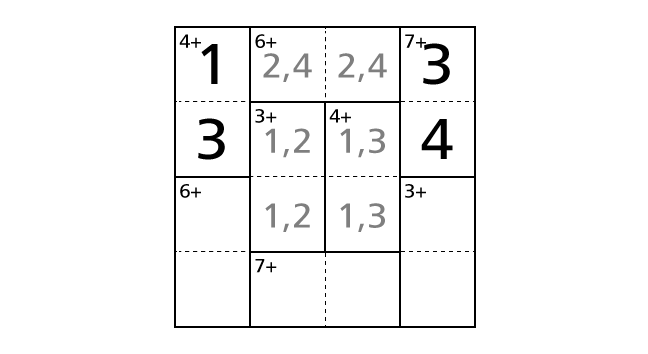
Process 5
Now we said that we cannot decide in which box to place a number 1. But, in fact, we can decide it by considering the fact that we placed a number 3 in box–(2,1). If we assume the case that we place a number 3 in box–(2,3) and a number 1 in box–(3,3), we notice that we end up violating the rule 1.
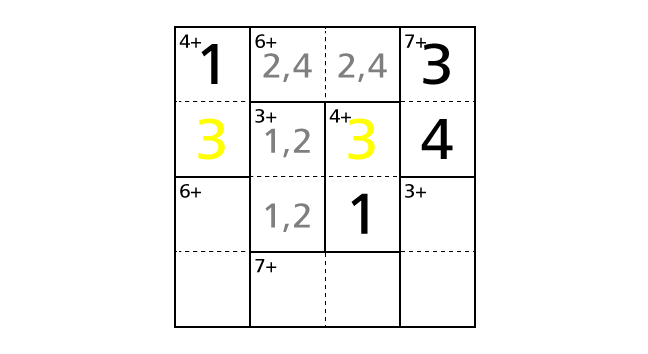
So we have to place a number 1 in box–(2,3) and a number 3 in box–(3,3) to avoid violating the rules. Now let’s place numbers.
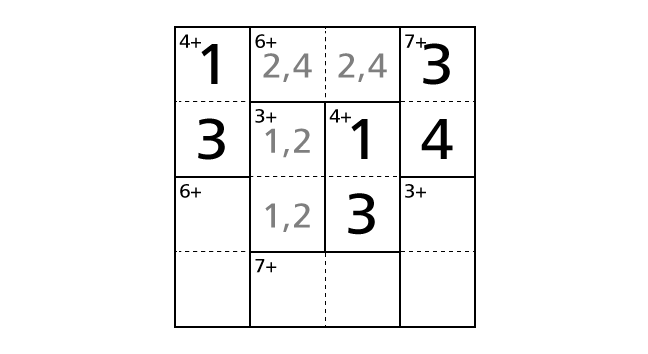
Process 6
Now we focus on row 2. By rule 1, we know that each row contains each digit of 1–4 exactly once. But number 1, 3 and 4 are already placed in row 2. So number 2 is the only choice to place in box–(2,2).

Let’s place numbers.
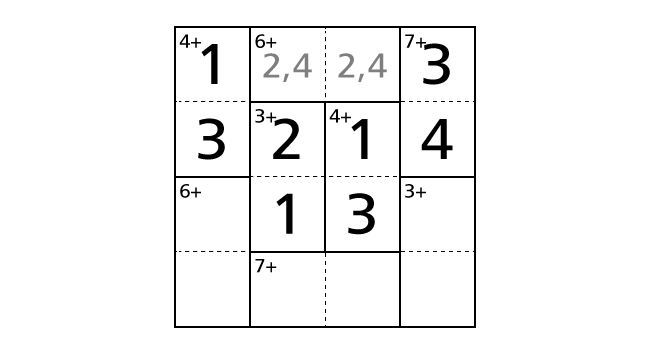
Process 7
Now we focus on the top center region including box–(1,2) and box–(1,3). If we assume the case that we place a number 2 in box–(1,2) and a number 4 in box–(1,3), we notice that we end up violating the rule 2.
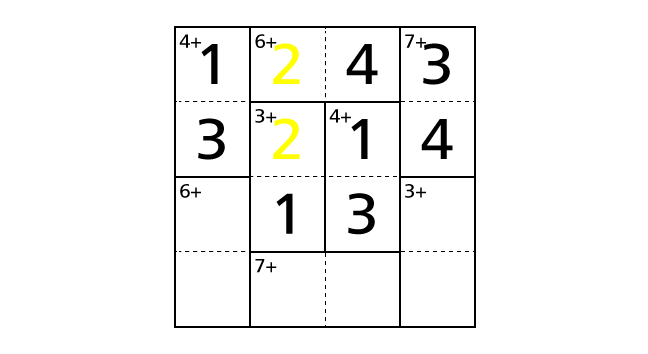
So we have to place a number 2 in box–(1,3) and a number 4 in box–(1,2) to avoid violating the rules. Now let’s place numbers.
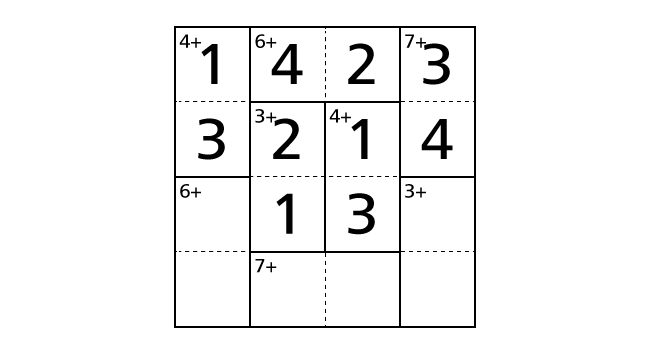
Process 8
We focus on column 2. By rule 2, we know that each column contains each digit of 1–4 exactly once. But number 1, 2 and 4 are already placed in column 2. So number 3 is the only choice to place in box–(4,2).
As the same way, we focus on column 3. By rule 2, we know that each column contains each digit of 1–4 exactly once. But number 1, 2 and 3 are already placed in column 3. So number 4 is the only choice to place in box–(4,3).

Let’s place numbers.
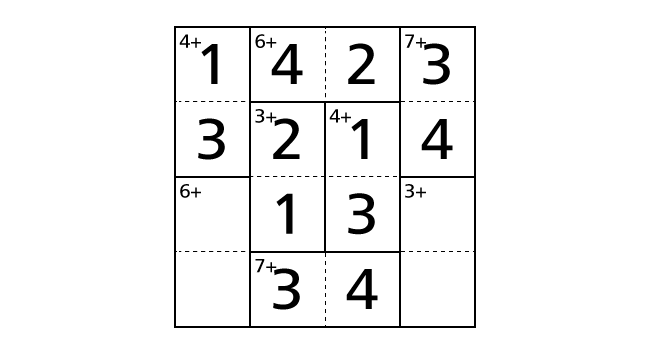
Here we note that we haven’t violated the rule 3 in the bottom center region including box–(4,2) and box–(4,3).
Process 9
Now we focus on the bottom left region including box–(3,1) and box–(4,1). Among four number from 1 to 4, 2 and 4 are the only combination that the result of the addition of two numbers becomes 6. Thus, we know that we have to place a number 2 and a number 4 in box–(3,1) and box–(4,1). But, from only this hint, we cannot decide in which box to place a number 2. So now we record this in boxes with light-colored characters.
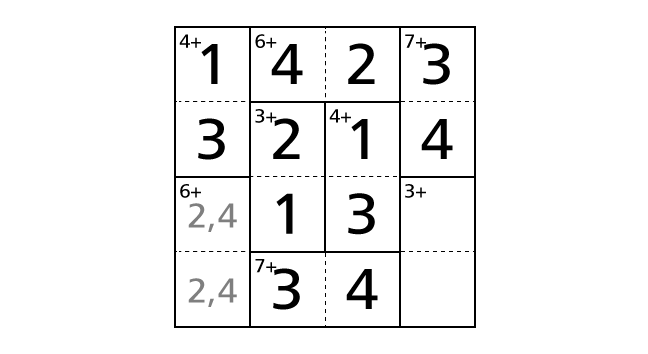
About this region, we assume the case that we place a number 2 in box–(3,1) and a number 4 in box–(4,1). Then we see number 4 twice in row 4. Thus this case ends up violating the rule 1.

So we have to place a number 2 in box–(4,1) and a number 4 in box–(3,1) to avoid violating the rules. Now let’s place numbers.
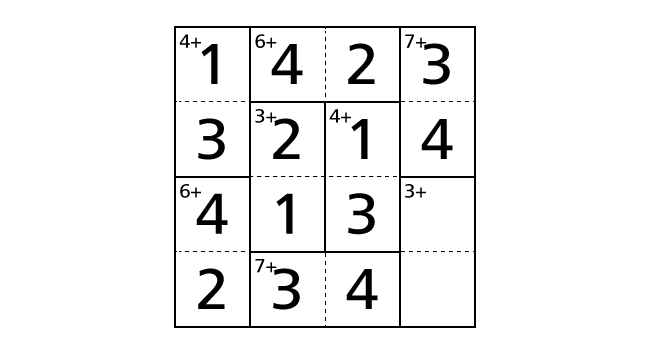
Process 10
Next, we focus on row 3. By rule 1, we know that each row contains each digit of 1–4 exactly once. But number 1, 3 and 4 are already placed in row 3. So number 2 is the only choice to place in box–(3,4).
As the same way, we focus on row 4. By rule 1, we know that each row contains each digit of 1–4 exactly once. But number 2, 3 and 4 are already placed in row 4. So number 1 is the only choice to place in box–(4,4).

Now let’s place numbers.
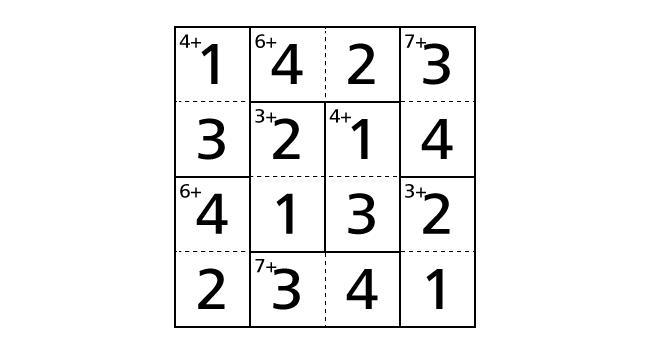
Here we note that we haven’t violated the rule 3 in the bottom right region including box–(3,4) and box–(4,4). Finally, we reached the answer.
Get Started
Most recently uploaded CalcBlocks puzzles are available on CalcBlocks.
Previous CalcBlocks puzzles are available on CalcBlocks Archives.
